Investigating tries: writing a spell-checking algorithm

This article walks through writing a spell-checking algorithm, making use of a neat data structure called a trie, which is particularly suited to the problem.

We will look at:

Problem

We wish to write a spell-checking algorithm which should return a boolean indicating whether the word might be valid or not. It should return false only if there is no possibility of the word being correct. Words which are incorrect but may be made correct with the addition of further letters should return true.

Let's consider some solutions using conventional data structures.

Tries

A trie is a data structure which can store strings in a way which makes them easy to search. The following diagram shows a trie with the strings app, apple and cat stored in it.

0 -> a -> p -> p. -> l -> e.
 `-> c -> a -> t.

In this diagram, 0 represents the node at the top of the trie, which has no value associated. Nodes marked are marked with a dot . to signify that they contain a letter which is at the end of a word.

The trie is made up of a series of interconnected nodes. Each node stores a single character, and interconnecting lines show the relationship between characters. By following the lines, we can see our three words

We can see that a trie explicitly encodes the characters of a word in its nodes, making it suitable for our spell-checking algorithm, where we need to be able to match substrings of words in the dictionary.

Our trie will need to support two operations:

Implementation

First, let's implement our trie. Tries consist of a series of nodes. Each node must store a value, a record of the child nodes, and whether the node points to the end of a complete word.

The child nodes can be stored in different ways, depending on the properties desired in the trie. Here, we store them in a dict, which offers fast O(1) lookup times, but require larger memory usage. A list could alternatively be used to reduce memory usage, at the cost of slower lookup time.

Using a dict, the algorithmic complexity of spell-checking a word should be O(m), where m is the length of the string being checked3.

class Node(object):
   def __init__(self, value=None):
        self.value = value
        self.children = {}
        self.is_complete = False

The trie itself just contains a reference to the top of the string of nodes:

class Trie(object):
    def __init__(self):
        self.node = Node()

We can now implement the insert method:

class Trie(object):
    # ...
    def insert(self, key):
        node = self.node
        for letter in key:
            if letter in node.children:
                node = node.children[letter]
            else:
                new_node = Node(letter)
                node.children[letter] = new_node
                node = new_node
        node.is_complete = True

Insert takes a key to insert, iterates over it, and adds each letter to the trie, creating new nodes if necessary.

search method:

class Trie(object):
    # ...
    def search(self, key):
        node = self.node
        for letter in key:
            if letter not in node.children:
                return False
            else:
                node = node.children[letter]
        return True

Search iterates over the letters in the key, checking that each node contains a child whose value matches the letter.

Analysis

We can compare how our trie-based algorithm compares to binary search which by running a benchmark test. The test searches for 1000 randomly selected words from the dictionary 100 times each.

$ python benchmark.py
Binary search 1000 items 100 times: 2.32307600975
Trie search 1000 items 100 times: 0.461572885513

Complexity

We can empirically measure the algorithm's time complexity by measuring the time taken to search for words of variable length known to be in the trie.

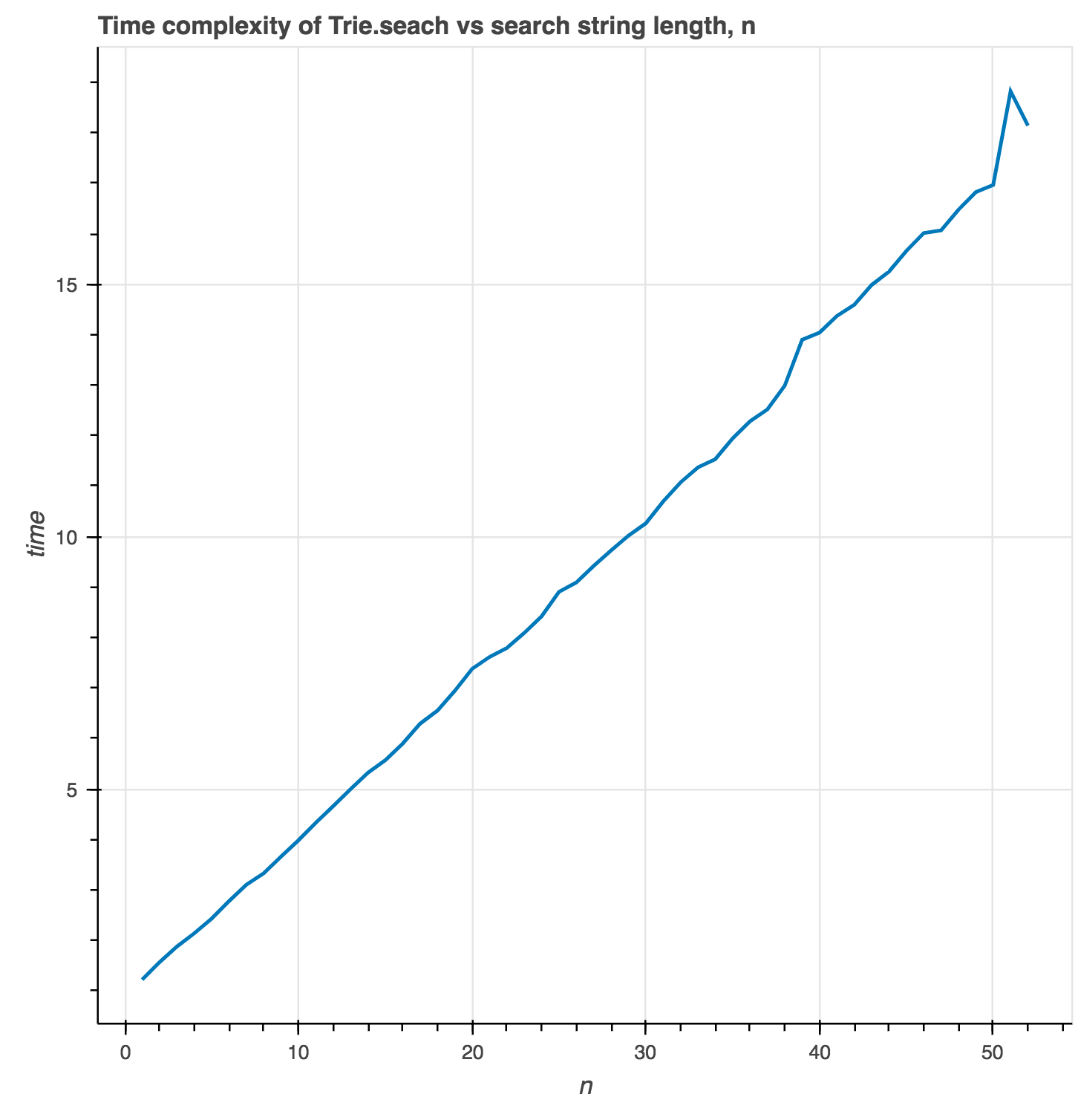
Graph showing trie's search has linear time complexity.

Trie.search has linear time complexity, as expected.

Improvements

Speed up searching successive characters in a word

When spell-checking, a word as it is typed, we make multiple calls to the search() function, each time passing the previously searched value with a new character appended. For example, when typing the word 'word', the following searches are made:

When searching for 'wor', you repeat the work done when searching for 'wo' and 'w'. We can modify our algorithm to take this into account:

class Trie(object):
    # ...
    def search(self, key, prev_node=None):
        node = prev_node if prev_node is not None else self.node
        for letter in key:
            if letter not in node.children:
                return False, node
            else:
                node = node.children[letter]
        return True, node

In this code, the last searched node is returned to the caller. The caller can then supply this node when calling search with the next character in the word to continue searching when we left off.

Startup time

One disadvantage of this algorithm is that initialising the trie takes some time. By profiling the insertion of the dictionary into the trie, we can see that a lot of this time is spent initialising Node objects:

$ python profile_trie_insert.py
     1028667 function calls in 5.354 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     1    0.176    0.176    5.354    5.354 <string>:1(<module>)
     1    0.101    0.101    5.178    5.178 profile_trie_insert.py:6(initialise_trie)
792777    3.273    0.000    3.273    0.000 trie_dict.py:12(__init__)
     1    0.000    0.000    0.000    0.000 trie_dict.py:20(__init__)
235886    1.804    0.000    5.077    0.000 trie_dict.py:29(insert)
     1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

This startup time could be improved by implementing Node with an object with one which is faster to initialise, such as a collections.namedtuple.

However, this slow startup only needs to be run once, and won't affect performance once initialised.

Memory usage

Tries trade off speed for memory usage. Although storing a list of words in a trie reduces the total number of characters stored4, each character stored now has overhead associated with it from the Node object which contains it, and the dict used to store its relationships.

This memory usage can be reduced by storing the words in a deterministic acyclic finite state automaton, which prunes some of the redundancy out of the trie.

Extensions

Tries can be used in similar ways to implement:

Perform binary search, but instead of searching for the string in the dictionary which == the search term, search for a string which startswith() the search term.

We are not just searching for a word in a dictionary, but also for words which could have letters added them to make them valid. We can do this by checking whether the dictionary entry starts with the letters of the search term O(m) at each step of the search O(log n)

At each step of the seach, we do a dict key lookup, which is O(1). For a word with m characters, we perform m of these lookups, giving an overall search complexity of O(m).

Storing the words 'cat' and 'cab' in a list requires storing six characters. In a trie, we only store four:

  c -> a -> t
        `-> b
  1.  ↩︎
  2.  ↩︎
  3.  ↩︎
  4.  ↩︎